3.
Fractions
Many children (and adults for that matter) find fractions difficult to understand. This is often because fraction notation (writing a fraction as a number, e.g. ½ ) is very confusing. Children therefore struggle to relate the symbol to the ‘thing’ and end up guessing. In Singapore, the understanding of fractions is rooted in the Concrete, Pictorial, Abstract (CPA) model, where children use paper squares and strips to learn the link between the concrete and the abstract.
At the heart of understanding fractions is the ability to understand that we’re giving an equal part a name. It is simply a naming activity!
1. Finding equal parts
Children need to understand what a fraction is. When we divide a whole into equal parts we create fractions. A fraction is just an equal part.
2. Naming equal parts
Once the children can make/identify equal parts (fractions), they need to give them a name.
For example: children cut a pizza into a different number of equal parts. To show that the equal parts are different, the children give them different names. Each part might be 1 third, or each part might be 1 quarter or 1 fourth. This is the denominator (name).
3. Operations involving equal parts
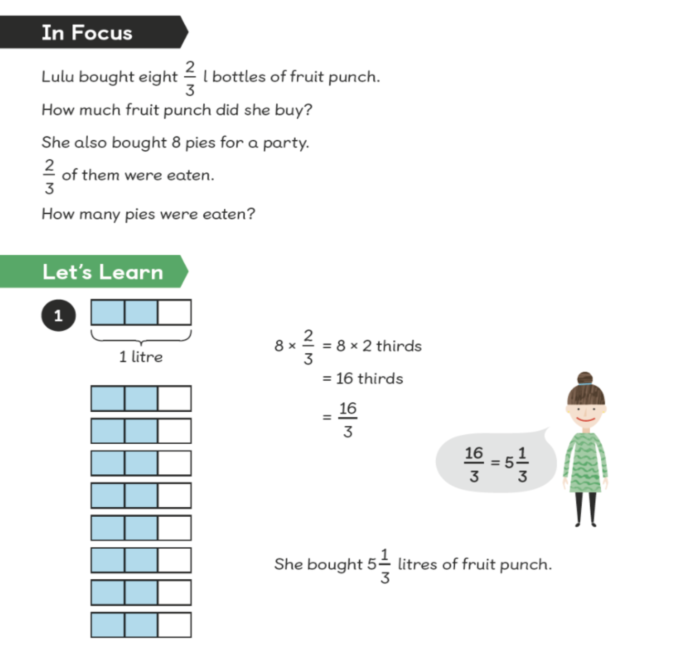
If children can name a fraction, they are ready to do calculations using like fractions (they have the same name).
For example: children use strips of paper to model the problem and see how it links to the written and symbolic notation.
4. What if the parts aren’t equal?
Can we add 3 apples and 2 oranges? Is it 5 apples? Is it 5 oranges? It is neither because we cannot add things with different names. We have to give them the same name, and in this case we could rename them as ‘fruit’. They now all have the same name and so we can do the calculation (5 pieces of fruits). The same is true for fractions. We can’t add 2 quarters and 1 eighth because they have different names, however, if we can give them the same name (equivalent) it is possible.
For example: children cut up a quarter to show more equal parts and name the parts.
Finding Equivalent Fractions:



